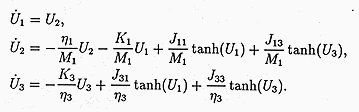
One of the most interesting new topics in physics in recent decades is the dynamics of neural networks. Neural networks are simplified models of brain cells in interaction with each other. Each cell is called a neuron, and many of the basic properties of how neurons interact with each other in the human brain can be investigated using electronic models.

Professor W.C. Schieve and his students have examined certain two-, three-, and four-neuron networks using coupled differential equations, like the ones shown at left. Even for these small systems, behavior of the electronic current in the neural network can be very complex, and even chaotic.

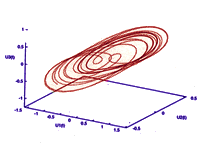
The diagram at left shows an example plot of the dynamics of a two-neuron system. The trajectory is an example of a limit cycle, and it shows how stability can arise in many-neuron systems despite the complex dynamics of the system.

Prof. Schieve's recent articles on neural networks have appeared in several journals, including the Physical Review.