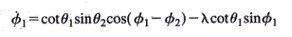
| Main Page |
Overview
| Research at the Center
|
| 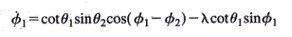
| Chaos in Quantum and Classical Spin Systems
For classical nonlinear systems, it is possible to use a wide variety
of numerical and analytical techniques to investigate dynamical behavior.
For the quantum version of these same nonintegrable systems, however, it is
not possible to use these same techniques in most cases, and thus new methods
must be found. One of the most promising such techniques to study quantum chaos is the plotting of a "web of simultaneous eigenstates."
One of the most interesting such quantum models is the two-particle
system with spin interaction. The system with spin interaction has long
been considered one of the most formidable in dynamics, because the interaction is a strong coupling. That is, it cannot simply be considered as a small perturbation on the case of free particles. The classical equation of motion of this system is shown at left.
|
|
| 
| For the classical case of two particles with magnetic moments, it is possible
to study the dynamics by means of the conventional technique of the Poincaré Surface of Section, as shown at left. One of the most interesting features of this system is that the system is chaotic for intermediate values of the coupling parameter. At higher values, the chaos disappears completely because of the strong nature of the interaction.
|
|
| 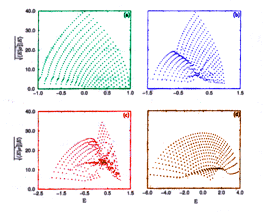
| Dr. Linda Reichl and Daniel Robb have recently investigated the quantum chaotic properties of this same system using a the web of simultaneous eigenstates technique [Phys. Rev. E57, (1998) p.57]. From the diagram at left, it is apparent that in the quantum case, this system has many of the same features as its classical counterpart. Namely, the array of eigenstates is regular at low values of the coupling parameter, becomes chaotic at intermediate values, and then becomes regular once again for stronger values of the coupling.
|
|
| Figure by
Daniel T. Robb.
|
by Matthew A. Trump
Back to the Main Page
| |