
A Glimpse Inside at the Center's Research
Romanian translation

|
The Ilya Prigogine Center for Studies in Statistical Mechanics and
Complex Systems A Glimpse Inside at the Center's Research Romanian translation |
| For many years, the research at the Ilya Prigogine Center has been regarded as among the finest and most advanced in the world, particularly in the field of theoretical and computational dynamics. The wide umbrella of research topics at the center includes quantum and classical statistical mechanics, many-body dynamics, and thermodynamics. In addition, the Center is regarded worldwide as one of the most important research facilities for study of chaotic motion, in physical, biological, and economic systems. |

|
 |
One of the important objectives of the research at the Center is the study of
nonequilibrium processes and a fundamental understanding of the irreversible flow of time. The research
into irreversible systems is lead by
Ilya Prigogine (pictured above), the 1977 winner of the Nobel Prize in Chemistry,
whose work has been been regarded as the among the most
influential on this topic for many decades. Dr. Prigogine's thoughts on the role of time in physics
have lead the way for a generation of research into complex systems. In the broad picture, the work of Prof. Prigogine and his co-workers may be regarded as the most extensive on-going attempt to find the source of irreversibility in the laws of physics. Because the fundamental laws of physics from the time of Newton have always been time-reversible, the question of why we as human beings should experience a definite direction in time has not been resolved. Prof. Prigogine has long believed that it may be necessary to broaden the scope of the fundamental dynamical laws to include solutions that are irreversible in time. In the past decade, members of the Center have explored important new numerical and analytical means by which time-irreversibility can arise in dynamical systems. One of the most intriguing such avenues explored by the Center is the use of probability distributions, rather than trajectories, to describe the evolution of complex systems. Whereas the traditional dynamical equations using trajectories are time-reversible, and thus cannot describe irrerversible evolution, the equations governing the evolution of probability distributions have exact solutions that are not time-reversible. Prof. Prigogine and his co-workers have been at the forefront in the exploration of the use of probability density equations in dynamics. One of the Center members most involved in this effort is Center fellow Dr. Dean Driebe. Working alongside Dr. Prigogine, Dr. Driebe has constructed new solutons of the time evolution operators for a variety of chaotic dynamical systems. These new solutions involve generalized functions that explicitly break the time symmetry. The sequence of diagrams to the left are from Dr. Driebe's work and appear in Dr. Prigogine's latest book.From top to bottom, the panels show the effect of the Bernoulli map on a probability distrubtion which is initially uneven, as in the purple panel at the top. Downward, as time increases, the effect of the Bernoulli map, a simple one-dimensional chaotic system, on the initial distribution is to smoothen it out into an even distibution, i.e., the equilbrium density in red. Dr. Prigogine has advocated the view that the fundamental laws of physics must be in terms of probability distributions--rather than the trajectories used since the time of Newton. Much of the Center's ongoing research involves the attempt to broaden the laws of physics to incorporate dynamical solutions which are time irreversible. The recent developments in the understanding of deterministic chaos offers exciting new avenues of research in this field, one in which several Center members are regarded as leaders.
|
| Prof. Prigogine and his co-workers have also studied methods by which irreversibility may arise in collisions of three bodies. Although two-body collisions obey a rather straight-forward dynamical law, three-body collisions do not, and the dynamics of these interesting processes is still only partially understood. Center research scientist Dr. Tomio Petrosky and postdoctoral fellow Dr. Gonzalo Ordoñez have recently performed groundbreaking numerical simulations of three-body scattering processes using probability distribution methods rather than trajectories. Their work indicates that solutions exist for the time evolution of the probability distribution which do not arise in trajectory dynamics, possibly indicating a signature by which irreversibilty arises in three-body dynamics. The diagram at right was created by Dr. Ordoñez to indicate these solutions. The axes of the diagram are a special type of coordinates, called Jacobi coordinates, based on the speeds of the three particles which collide. The diagram shows the probability distribution in the Jacobi coordinates at a certain instant in time near the moment when the three bodies collide. Red indicates the highest density, blue the least. The most interesting feature in the diagram in the bright horizontal "twin bar" passing through the middle of the plot. This feature is present only if certain probability distributions are used to describe the system. It disappears if trajectory dynamics used. Thus the presence of the bar in the plot may be a "signature" of probability distribution dynamics in nature. For more information on the Center's research on three-body collision, see Dr. Ordoñez's online description. | 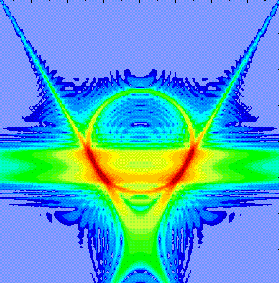
|
|
In addition to the work of Dr. Prigogine and his co-workers, the Center's work
includes the renowned work of both
Prof. Linda Reichl and
Prof. William C. Schieve. Dr. Reichl and her co-workers have made significant
contributions in the study of quantum chaotic systems. Dr. Schieve and his co-workers
have explored the complex dynamics of quantum statistical systems
and neuron dynamics. In addition, Dr. Schieve is regarded as one of the
world experts in the field of relativistic
chaos. One of the important missions of the Center also concerns education. In addition to the undergraduate and graduate courses taught by the aforementioned faculty members, the physics education outreach work of Dr. Jack Turner is regarded as one of the most significant and influential in the City of Austin and throughout the State of Texas. | |
|
Back to the Center Homepage
|
|